mcua

Movimiento circular uniformemente acelerado

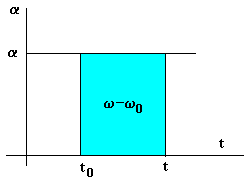	Un movimiento circular uniformemente acelerado es aquél cuya aceleración a es constante.Dada la aceleración angular podemos obtener el cambio de velocidad angular w -w0 entre los instantes t0 y t, mediante integración, o gráficamente.
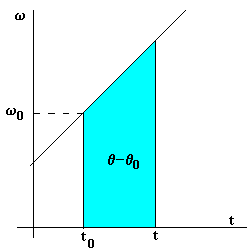	Dada la velocidad angular w en función del tiempo, obtenemos el desplazamiento q -q0 del móvil entre los instantest0 y t, gráficamente (área de un rectángulo + área de un triángulo), o integrando

Habitualmente, el instante inicial t₀ se toma como cero. Las fórmulas del movimiento circular uniformemente acelerado son análogas a las del movimiento rectilíneo uniformemente acelerado.

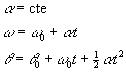
Despejando el tiempo t en la segunda ecuación  y sustituyéndola en la tercera, relacionamos la velocidad angular ω con el desplazamiento θ-θ₀

PROBLEMAS:

1.- Una rueda de 50cm de diámetro tarda 10 segundos en adquirir una velocidad constante de

360rpm. 

a) Calcula la aceleración angular del movimiento. 

b) Cuando la rueda llega a la velocidad anterior, ¿cuál es la velocidad lineal de un punto de la periferia? 

c) Calcula la aceleración centrípeta que posee a los 5 segundos la rueda del problema.

Datos:

Radio = 0,25m

ω0 = 0 rad/s

ωf = 360rpm = 120π rad/s

t = 10 s

a) Para hallar la aceleración angular, usaremos la fórmula de la velocidad angular del MCUA:

ωf = ω0 + α·t 

120π = α·10

 α = 12π rad/s2

b) Cualquier magnitud lineal puede calcularse a partir de su correspondiente angular

multiplicándola por el radio, por lo que

v = ω·R

v = 120π · 0,25 = 94,25 m/s

c) La aceleración centrípeta (o normal) es igual a la velocidad lineal al cuadrado dividida entre el

radio. Para sacar la velocidad lineal a los 5 segundos, tenemos que hallar la velocidad angular a los

5 segundos, usando la misma fórmula que en el apartado a)

ωf = 12π ·5 = 60π rad/s

v = 60π·0,25 = 47,12 m/s

an = (47,12)2

/0,25 = 8882,64 m/s2

 2.-Un hombre hace girar una honda desde el reposo durante 10 segundos con una aceleración

angular de π radianes/s2

, momento en el cual suelta la cuerda para dejar salir el proyectil. ¿A qué

velocidad sale despedido este si la cuerda de la honda mide 60cm?

Datos:

t = 10s

α = π rad/s2

ω0= 0 rad/s

Primero tenemos que hallar la velocidad angular final al cabo de esos 10 segundos:

ωf = ω0 + α·t 

ωf = π ·10 = 10π rad/s

Por lo que la velocidad lineal será:

v = 10π·0,6 = 18,85 m/s